ABE考核
2025.06.05-Charm-Crypto库环境配置
2025.06.06-布尔访问树算法
2025.06.06-线性秘密共享方案
2025.06.06-拉格朗日差值实现秘密恢复
2025.06.07-基于cpabe的医院场景加密解密demo方案
2025.06.08-基于Chram-Crypto库的医院场景CpabeDemo实现
本文档使用 MrDoc 发布
-
+
首页
2025.06.06-拉格朗日差值实现秘密恢复
#### 拉格朗日插值多项式 对某个多项式函数,已知有给定的 $$k+1$$ 个取值点:$$(x_0, y_0), (x_1, y_1), \ldots, (x_k, y_k)$$,其中 $$x_j$$ 对应着自变量的位置,而 $$y_j $$对应着函数在这个位置的取值。假设任意两个不同的 $$x_j $$都互不相同,那么应用拉格朗日插值公式所得的拉格朗日插值多项式为: $$f(x) = \sum_{j=0}^{k} y_j l_j(x)$$ 其中的$$ l_j(x)$$称为拉格朗日插值基函数,其表达式为: $$l_j(x) = \prod_{i=0, i \neq j}^{k} \frac{x - x_i}{x_j - x_i} = \frac{(x - x_0)}{(x_j - x_0)} \cdots \frac{(x - x_{j-1})}{(x_j - x_{j-1})} \frac{(x - x_{j+1})}{(x_j - x_{j+1})} \cdots \frac{(x - x_k)}{(x_j - x_k)}$$ 例如:我们考虑任意的三个点:$$(x_0, y_0) = (1, 6), (x_1, y_1) = (2, 11), (x_2, y_2) = (3, 18) $$带入 $$l_j(x) $$计算得到 $$l_0 = \frac{x - 2}{1 - 2} \frac{x - 3}{1 - 3} = \frac{1}{2} x^2 - \frac{5}{2} x + 3$$ $$l_1 = \frac{x - 1}{2 - 1} \frac{x - 3}{2 - 3} = -x^2 + 4x - 3$$ $$l_2 = \frac{x - 2}{5 - 2} \frac{x - 4}{5 - 4} = \frac{1}{2} x^2 - \frac{3}{2} x + 1$$ 最后带入 $f(x)$ 得到插值多项式: $$f(x) = \sum_{j=0}^{2} y_j l_j(x)$$ $$= 6 \left( \frac{1}{2} x^2 - \frac{5}{2} x + 3 \right) + 11 \left( -x^2 + 4x - 3 \right) + 18 \left( \frac{1}{2} x^2 - \frac{3}{2} x + 1 \right)$$ $$= 3 + 2x + x^2$$ #### 以下图所示的访问树为例,实现秘密共享与恢复 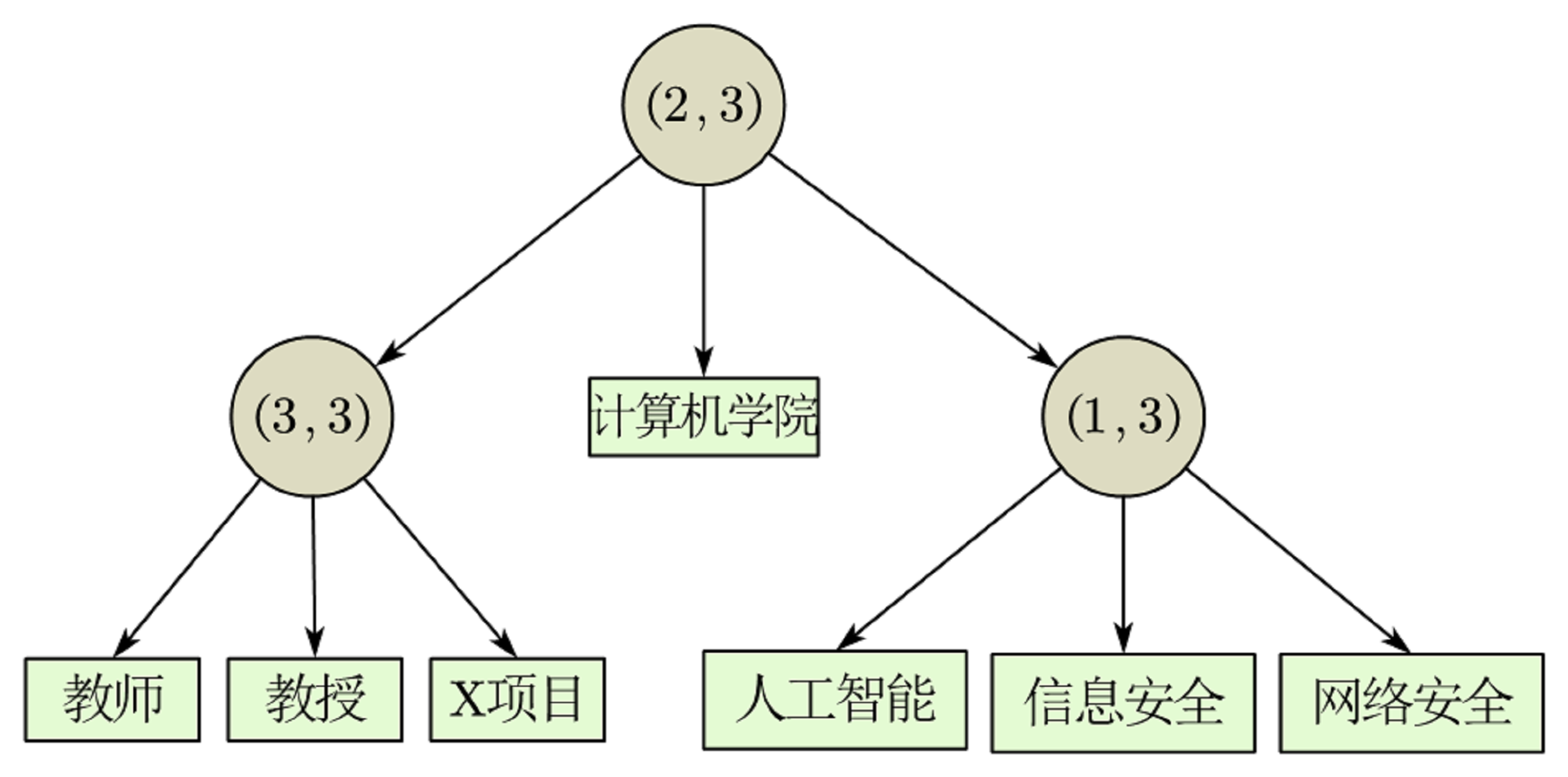 ``` from src.node import * # 先构造叶子节点 t33 = Node.threshold_node(Gate(3, 3), [Node.attr_node('教师'), Node.attr_node('教授'), Node.attr_node('X项目')]) t13 = Node.threshold_node(Gate(1, 3), [Node.attr_node('人工智能'), Node.attr_node('信息安全'), Node.attr_node('网络安全')]) # 构造root t23 = Node.threshold_node(Gate(2, 3), [t33, Node.attr_node('计算机学院'), t13]) print(t23) ''' (2, 3): None (3, 3): None 教师: None 教授: None X项目: None 计算机学院: None (1, 3): None 人工智能: None 信息安全: None 网络安全: None ''' ``` #### Shamir秘密共享 假设某个秘密值为10.0,从根节点开始共享,所有非叶子节点的多项式常数均为来自父节点的秘密分片,在递归的过程中,自变量x的值就是孩子节点从左至右的序号,为了方便计算,我们假定所有多项式的非常数项系数均为1 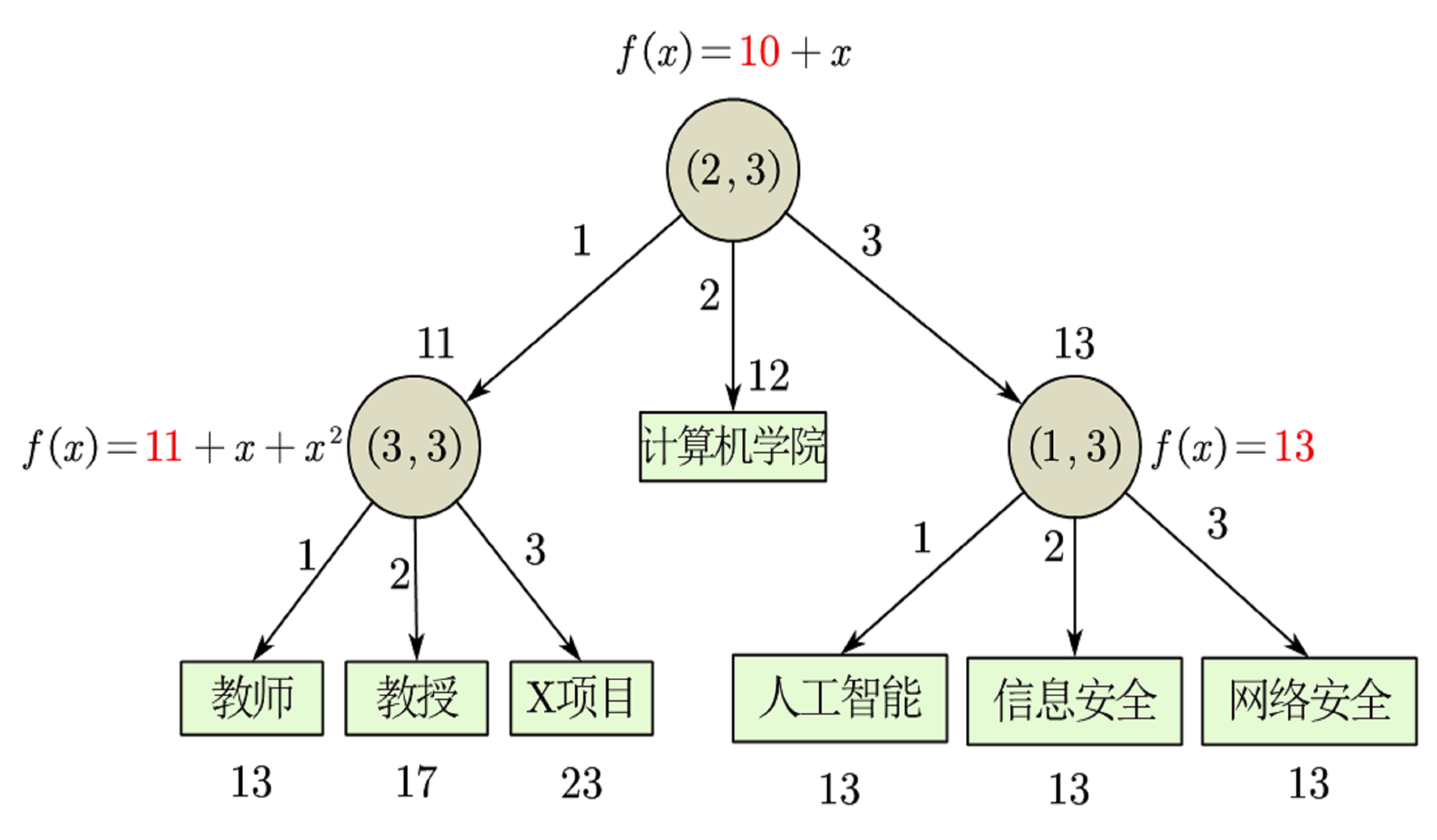 代码传入参数为访问**控制树的根节点以及秘密S**,代码中的多项式的系数为随机化,在range(1,101) 例如: 如果一个门限节点是 (2, 2): * 它会构造一个一次多项式 f(x) = ax + s,其中 a 是随机生成的。 * 它的两个子节点分别获得 f(1) 和 f(2)。 * 任何一个子节点拿不到另一个节点的 share,就无法还原 s,符合门限性质。 ``` def secret_share(root: Node, s): """ 递归分享秘密值 """ root.secret = s # 将秘密 s 分配到当前节点(不论是否叶子节点) if not root.is_leaf(): # 如果不是叶子节点(即是门限节点),则需要构造一个多项式进行秘密分享 # 构造一个随机多项式 coef: # - 该多项式的常数项为秘密 s(即 coef[-1]) # - 其余 k-1 项为随机生成的整数,范围 1~100 coef = np.append(np.random.choice(range(1, 101), size=(1, root.gate.k - 1)), s) # 下面对每个子节点进行秘密分配 # enumerate 从 1 开始,是为了匹配 Shamir 方案中第 i 个点的 x 值为 1, 2, 3, ... for x, c in enumerate(root.children, 1): # 使用多项式 coef 计算第 x 个点上的值,即秘密片段 share = np.polyval(coef, x) # 递归地将该秘密片段分配给子节点 secret_share(c, share) ``` ``` s = 10.0 secret_share(t23, s) print(t23) ''' (2, 3): 10.0 (3, 3): 51.0 教师: 229.0 教授: 585.0 X项目: 1119.0 计算机学院: 92.0 (1, 3): 133.0 人工智能: 133.0 信息安全: 133.0 网络安全: 133.0 ''' ``` #### 秘密恢复 在恢复的过程中,从叶子结点开始,自底向上递归恢复, * **对于叶节点来说,如果它的属性在用户属性列表里面,则视为满足**, * 对于**非叶子节点来说,如果叶子结点的满足的个数大于等于k,则视为满足**, * **此时进行拉格朗日插值计算多项式在x = 0处的函数值,并将其赋值给其自身的秘密值** * 最终,恢复出来的秘密值保存在根节点下。在回复之前,我们首先将所有非叶子节点的秘密值置为None。 ``` def secret_clear(root: Node): if not root.is_leaf(): root.secret = None for c in root.children: secret_clear(c) def secret_recover(root: Node, attrs): if root.is_leaf(): if root.attr in attrs: print(f'属性: \'{root.attr}\' 满足!') return True else: print(f'属性: \'{root.attr}\' 不满足!') return False else: points = [] # 所有满足的子节点集合 for i, c in enumerate(root.children, 1): if secret_recover(c, attrs): points.append((i, c.secret)) if len(points) == root.gate.k: x, y = zip(*points) # 拉格朗日插值 poly = lagrange(x, y) root.secret = poly(0) return True return False ``` #### 测试 ``` attrs = ['教师', '教授', 'X项目', '信息安全'] # recover success # attrs = ['教师', '教授', '信息安全'] # recover failed # clear non-leaf node secret_clear(t23) # secret recover assert secret_recover(t23, attrs), '秘密恢复失败' print('秘密恢复成功,秘密值为:', t23.secret) ``` ``` 属性: '教师' 满足! 属性: '教授' 满足! 属性: 'X项目' 满足! 属性: '计算机学院' 不满足! 属性: '人工智能' 不满足! 属性: '信息安全' 满足! 秘密恢复成功,秘密值为: 10.0 ``` #### 双线性配对性质 1. 双线性性 * 对于任意 $$a, b \in \mathbb{Z}_p$$,有:$$e(g_1^a, g_2^b) = e(g_1, g_2)^{ab}$$ * 特别地:$$ e(g_1^a, g_2) = e(g_1, g_2)^a$$;$$ e(g_1, g_2^b) = e(g_1, g_2)^b$$ 这个性质是构建各种基于指数的方案(如ABE、签名)的核心。 2. 群同态性 * 对于 $$u_1, u_2 \in G_1$$,$$v \in G_2$$,有: $$e(u_1 \cdot u_2, v) = e(u_1, v) \cdot e(u_2, v)$$ * 对右边也成立:$$e(u, v_1 \cdot v_2) = e(u, v_1) \cdot e(u, v_2)$$ 说明配对是两侧同态映射(双线性映射的子性质)。
happyboysrt
2025年6月6日 20:42
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
PDF文档(打印)
分享
链接
类型
密码
更新密码