ABE考核
2025.06.05-Charm-Crypto库环境配置
2025.06.06-布尔访问树算法
2025.06.06-线性秘密共享方案
2025.06.06-拉格朗日差值实现秘密恢复
2025.06.07-基于cpabe的医院场景加密解密demo方案
2025.06.08-基于Chram-Crypto库的医院场景CpabeDemo实现
本文档使用 MrDoc 发布
-
+
首页
2025.06.06-线性秘密共享方案
#### 算法介绍 在算法开始阶段,将树的根节点标注一个长度为1的向量(1),初始化一个全局变量**counter=1**。并按照如下算法进行**广度优先遍历**: 1. 如果父节点是一个标注着向量‘或’的OR门限 * 将它的两个**子节点标注为v** * 保持**counter不变** 2. 如果父节点是一个标注着向量‘与’的AND门限 * 将v的**末尾用0填充**,使得v的长度变为counter * 右子节点用**v || 1**标注 * 左子节点用(**0,......,0)||-1标准**,(0的个数为counter) * counter++ #### 举个例子 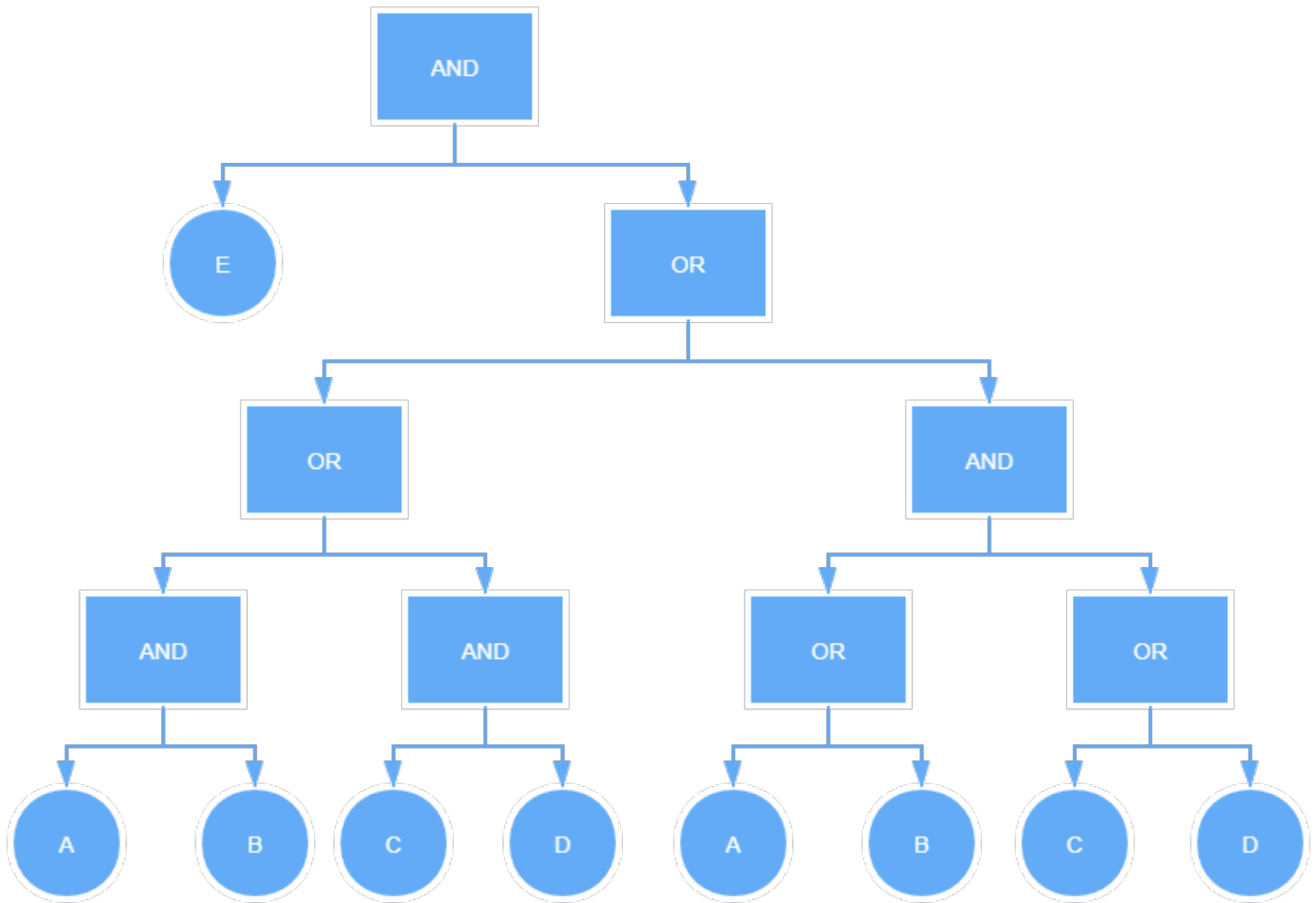 根据上述算法计算可以得到这个布尔访问树对应的LSSS矩阵为: ``` [[ 0 -1 0 0 0] [ 0 0 0 -1 0] [ 1 1 0 1 0] [ 0 0 0 0 -1] [ 1 1 0 0 1] [ 0 0 -1 0 0] [ 0 0 -1 0 0] [ 1 1 1 0 0] [ 1 1 1 0 0]] ``` #### 求解代码 代码传入参数为布尔访问树的根节点root,输出访问控制矩阵m; matrix = lewko_waters(root) darray = np.array(matrix) ``` # 布尔访问树转LSSS访问矩阵 from queue import Queue def lewko_waters(root): c, max_len, m = 1, 1, [] q = Queue() root.attr = [1] q.put(root) while not q.empty(): tmp = q.get() v = tmp.attr max_len = max(max_len, len(v)) if tmp.is_leaf(): m.append(tmp.attr) continue lc, rc = tmp.children[0], tmp.children[1] if tmp.gate.k == 1: lc.attr = v rc.attr = v else: v += [0] * (c - len(v)) lc.attr = [0] * c + [-1] rc.attr = v + [1] c += 1 q.put(lc) q.put(rc) for row in m: row += [0] * (max_len - len(row)) return m ```
happyboysrt
2025年6月6日 17:50
转发文档
收藏文档
上一篇
下一篇
手机扫码
复制链接
手机扫一扫转发分享
复制链接
Markdown文件
PDF文档(打印)
分享
链接
类型
密码
更新密码